삼각형은 컴퓨터 그래픽스의 가장 기본적인 도형중 하나이다.
3D그래픽의 가장 작은 단위인 폴리곤만 해도 삼각형으로 이루어져 있다는 것을 알 수 있다.
삼각형은 세 개의 정점으로 이루어진다. 이 세 개의 정점 중 두 개의 정점을 잇는 선분을 변이라고 한다.

이 삼각형의 세 변중 두 개의 변이 이루는 각을 내각이라고 한다.
또한 삼각형의 세 내각의 합은 항상 180도 이다.
삼각형은 그 모양에 따라 다양한 이름을 가지고 있지만, 우리가 삼각함수에서 다루고자 하는 삼각형은 직각삼각형이다.
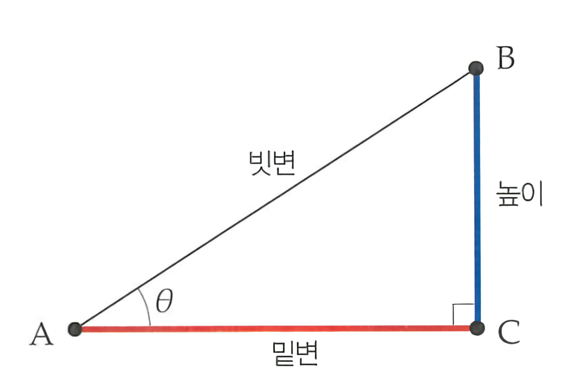
직각삼각형은 세 개의 정점 부분의 내각 중 하나가 직각을 이루는 삼각형을 말한다.

정점 C부분의 내각이 바로 직각이다.
또한 맞은편의 비스듬한 변 h를 빗변이라 하고, 바닥 b를 밑변, 마지막 a변을 높이라고 한다.
삼각함수란 직각삼각형에서 세 변의 길이와 빗변과 밑변이 이루는 내각의 각도 θ사이에 존재하는 관계를 이용하여 문제를 해결하는 것이 기본적인 사용법이다.
피타고라스 정리
피타고라스 정리는 흔히 A^2 = B^2 + C^2이라고 알려져 있다.
빗변의 길이를 a, 밑변의 길이를 b, 높이의 길이를 c라고 했을 때 성립한다는 의미이다.
삼각함수 - 사인, 코사인, 탄젠트
모두가 아는 삼각함수에 대해 알아보자.
직각삼각형에서 변을 두 개 선택한 경우 두 변의 길이의 비율은 θ의 각도에 따라 변화한다.
따라서 이 변화하는 매개변수 θ를 입력받아 출력되는 결괏값이 변화하는 함수 형식으로 각 변수 사이의 관계를 나타낼 수 있다.

사인의 정의는 다음과 같다.

sin θ는 각도가 세타일 때 빗변과 높이의 비율을 나타낸다.
빗변의 길이와 θ의 각도를 알고 있을 때 빗변의 길이에 θ를 곱하면 높이의 길이를 구할 수 있다.

반대로 사인의 역수를 이용하면 높이의 길이와 θ의 각도로부터 빗변의 길이를 구할수도 있다.
코사인의 정의는 다음과 같다.

코사인은 빗변과 밑변의 비율을 나타낸다.

빗변과 내각 θ가 있다면 빗변의 길이 cos θ를 곱해 밑변을 구할 수 있다.
탄젠트의 정의는 다음과 같다.
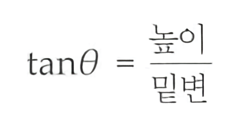
탄젠트는 밑변과 높이의 비이다.
또한 내각 θ를 매개변수로 받아 각 변끼리의 비율을 반환하는 사인, 코사인, 탄젠트에 대응해 그 역함수로서 각 변끼리의 비율을 매개변수로 하여 내각 세타의 각도를 구하는 일련의 함수도 있다.
바로 아크사인, 아크코사인, 아크탄젠트 이다.

이 함수를 이용하면 각각 사인, 코사인, 탄젠트 값으로부터 대응하는 각도 θ 를 산출할 수 있다.
'Programming > 기타' 카테고리의 다른 글
| 게임수학) 좌표계 - 2 (0) | 2024.11.18 |
|---|---|
| 게임수학) 좌표계 - 1 (1) | 2024.11.14 |
| 게임수학) 삼각함수 - 3 (0) | 2024.11.13 |
| 게임수학) 삼각함수 - 2 (1) | 2024.11.12 |
| 메모리 계층구조 (0) | 2024.09.24 |
