단위원
앞선 포스트에서 삼각함수는 매개변수 θ를 입력받아 출력되는 결과값이 변화하는 함수라고 설명했었다.
지금까지는 직각삼각형만을 염두에 두고 개념을 살펴보았지만 실제 삼각형은 θ값이 0~90도 사이에만 있는것은 아니다.
따라서 직각삼각형 뿐만 아니라 직각삼각형을 포함하는 원을 통해 삼각함수를 표현하는 방법에 대해 알아보자.

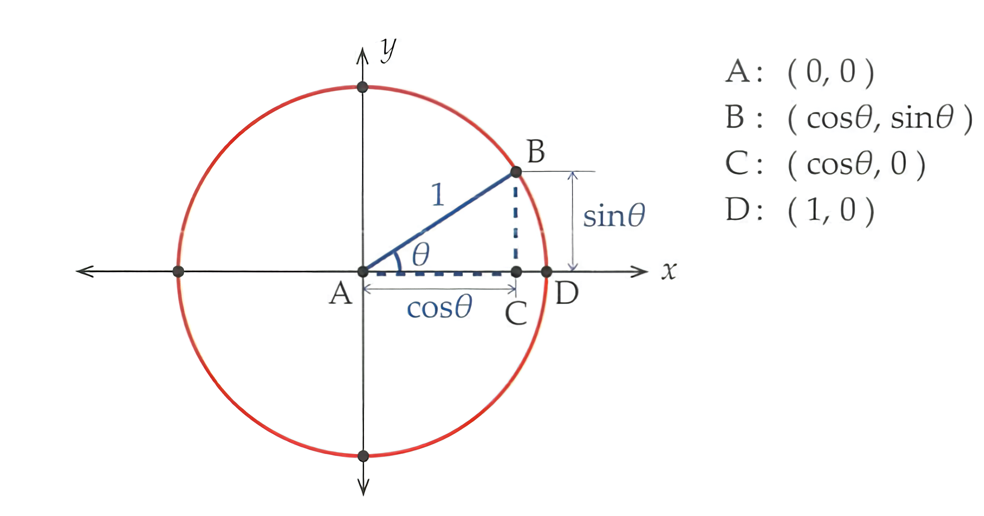
이 그림은 점 A를 중심으로 하는 반지름의 길이가 1인 단위원 위에 삼각형 ABC를 올려놓은 그림이다.
점 A를 중심으로 원 위의 점 B를 이어 선분 AB를 그린다면 당연히 선분 AB는 길이가 1이 될 것이다.
그리고 점 B에서 x축 방향에 수직으로 선을 그어 겹치는 부분을 점 C라고 하면 선분 AB와 선분 AC사이의 각, 다시말해 θ를 사인의 정의를 이용하여 구할수 있게 된다.
선분 BC와 AC의 길이는 보다 쉽게 구할수 있다.
코사인의 정의를 이용하면 선분 AC의 길이는 Cosθ가 되고, 사인의 정의를 이용하면 선분 BC의 길이는 Sinθ가 된다.
이제 삼각형 ABC에 피타고라스 정의를 적용해보면 다음과 같은 관계가 도출되게 된다.

이 단위원을 사용하여 여러가지를 할 수 있다.
원점을 축으로 원의 반지름을 회전시킴으로써 90도보다 큰 각도에서 삼각함수의 수치를 표현할 수 있다.

이런 식으로 θ만큼 점 P를 원 위에서 이동시키면 점 P의 x좌표는 Cosθ값을, y좌표는 Sinθ 값을 나타내게 된다. x좌표는 음수 위치에 있으므로 θ가 90~270도 사이에 있을 때는 코사인 값이 음수가 된다는 사실도 알 수 있다.
반대로 y좌표는 θ가 0~180도 사이에 있을 때는 양수, 180~360도 사이에서는 음수가 된다는 사실 또한 알수 있다.
이런식으로 사인, 코사인, 탄젠트가 xy평면의 각 사분면에서 양수와 음수 중 어느 쪽 부호를 갖는지 정리한 것이 바로 이 그림이다.

라디안
어느 한 원 위의 점이 원점을 중심으로 반지름의 길이만큼 한 방향으로 움직였을 때 대응하는 각의 크기를 1라디안이라고 한다. 라디안은 rad라고 하기도 하고, 그냥 1이라고 하기도 한다.
중요한 것은 반지름의 길이, 즉 180도를 1
코사인 법칙
이번에는 직각삼각형에서만이 아닌 일반 삼각형에서도 성립되는 성질에 대해서도 알아보도록 하자.

대강 이런 모양의 삼각형이 있다고 가정해보자.
q에서 pr에 수선을 내린 지점을 s라고 할수 있겠다. 당연히 수선을 내렸으니 직각삼각형 pqs는 피타고라스 정리를 이용하여 다음처럼 나타낼 수가 있다.

그 다음 우변을 전개해서 정리해주면 다음과 같은 식이 완성되게 된다.

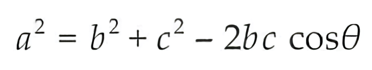
아마도 수학시간에는 이 식을 더 많이 보았을것이다.
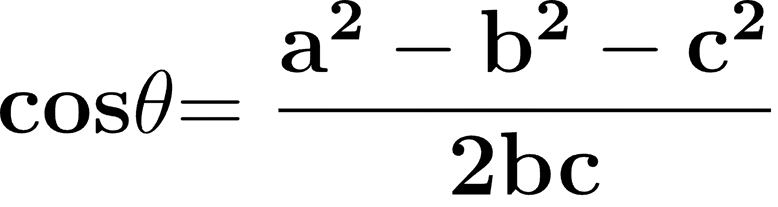
이 식을 코사인 법칙이라고 부른다.
코사인 법칙은 직각삼각형 뿐만 아니라 일반 삼각형에도 성립하는 성질이다.
피타고라스 정리는 코사인 법칙의 특수한 케이스이다.
'Programming > 기타' 카테고리의 다른 글
| 게임수학) 좌표계 - 2 (0) | 2024.11.18 |
|---|---|
| 게임수학) 좌표계 - 1 (1) | 2024.11.14 |
| 게임수학) 삼각함수 - 3 (0) | 2024.11.13 |
| 게임수학) 삼각함수 - 1 (0) | 2024.11.11 |
| 메모리 계층구조 (0) | 2024.09.24 |