극좌표계
이전 포스트에서 설명했었던 좌표계는 직교좌표계라고 하는 좌표계였다. 이 직교 좌표계와 다른 방식으로 물체의 위치를 표현하는 좌표계도 존재하는데, 그중 대표적인 극좌표계에 대해서 설명해보겠다.
극좌표계는 크게 2D와 3D로 구분할수 있다. 먼저 2D좌표계를 한번 알아보자.

마치 단위원처럼 생겼다는 것을 알 수 있다. 2D 극좌표계에도 직교좌표계처럼 중심에 극(Pole)이라고 불리는 기준점이 존재한다. 이 극에서 반지름처럼 극축이라고 불리는 반직선이 뻗어나오게 된다.
이 극좌표계에서 평면상의 점 P의 위치를 결정하는 방법은 극축과 P를 연결하는 직선 r의 길이와 극축과 r의 각도 θ를 통해 결정된다. 즉, 점 P의 극좌표는 (r, θ)가 된다는 것이다.
이 극좌표계라는 것은 보통 항공기나 선박의 네비게이션 용도로 활용되는데, 예를 들어 동쪽으로 5마일의 경우 90도로 5마일 이동하면 되는 식으로 사용한다고 한다.
극좌표계 또한 일종의 좌표계이므로 직교좌표계로의 변환 또한 가능한데, 이 경우 2D극좌표계에서 (r, θ)는 2D 직교좌표계에서는 (rCosθ, rSinθ)와 동일하다.
이미 단위원을 공부할 때 단위원 위의 점의 좌표를 구하는 법에 대해 공부했다면 왜 그런지는 알 수 있을 것이다.
반대로 2D직교좌표(x, y)를 극좌표로 표현하려면 조금 복잡해지는데, 자세한 풀이과정은 생략하도록 하겠다.
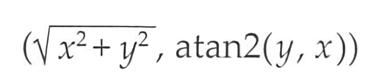
3D 극좌표계
직교좌표계에서 z축을 추가하여 3D 직교좌표계를 정의하는 것처럼, 극좌표에서도 축을 하나 더 추가하여 3D 극좌표계를 정의할 수 있다.
2D 극좌표에서는 반지름의 길이와 극축과의 각도로 정의했지만, 3D 극좌표계에서는 다른 하나의 축과 이루는 각도를 추가하여 총 3개의 값으로 좌표를 정의한다. 이 3D 극좌표계는 구면좌표계라고도 부른다.
3D 극좌표계를 최초로 알게 되는 시점은 아마도 지구과학 시간에 배우는 적도 좌표계일 것이다. 지구의 위치를 중심으로 상대적인 별의 위치를 표현하는 방식이다.
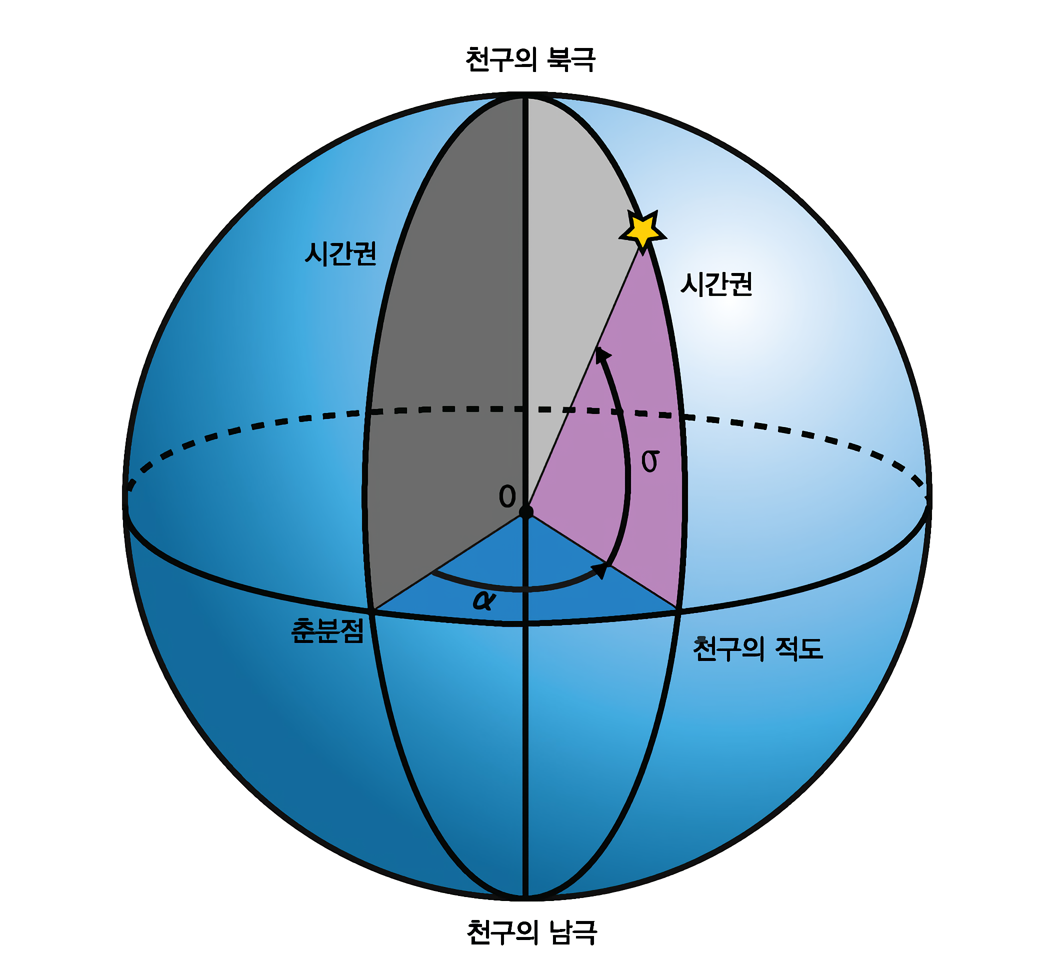
다음 그림처럼 적도 좌표계는 두 개의 각도를 사용하여 별의 위치를 표현한다. 즉, 반지름의 길이 한개와 각도 두 개를 사용하여 (r, θ, Φ)와 같은 식으로 표현한다.
'Programming > 기타' 카테고리의 다른 글
| 게임수학) 벡터 - 2 (0) | 2024.11.21 |
|---|---|
| 게임수학) 벡터 - 1 (0) | 2024.11.20 |
| 게임수학) 좌표계 - 1 (1) | 2024.11.14 |
| 게임수학) 삼각함수 - 3 (0) | 2024.11.13 |
| 게임수학) 삼각함수 - 2 (1) | 2024.11.12 |